Algebraisk geometri betegner undersøgelse af de geometriske figurer, der fremkommer som løsningsmængde til et system af algebraiske ligninger. Figurerne kan være algebraiske kurver eller flader. De mere generelle figurer kaldes også algebraiske mangfoldigheder.
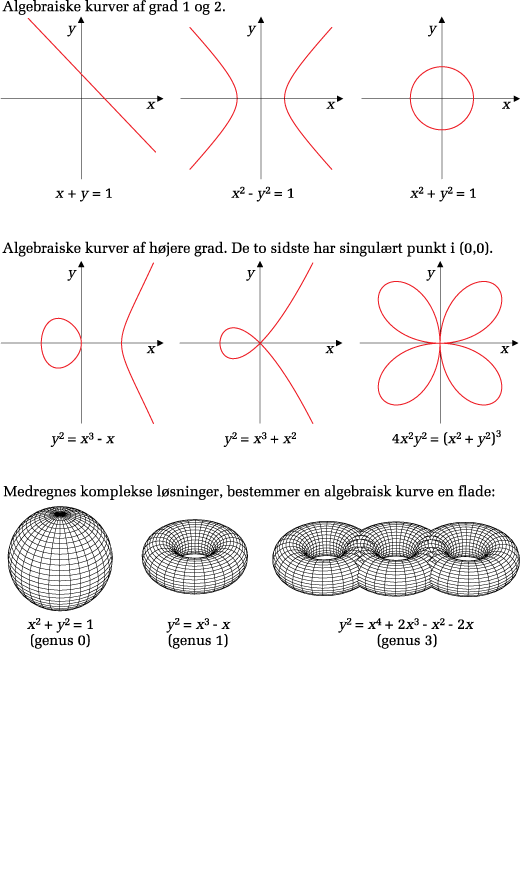
En algebraisk kurve i planen er således bestemt som mængden af punkter, hvis koordinater \((x,y)\) er løsninger til en ligning af formen \(f(x,y) = 0\), hvor \(f\) er et givet polynomium. Hvis polynomiet \(f\) er af grad \(1\), udgør løsningerne en ret linje. For polynomier af grad \(2\) bliver løsningsmængden et keglesnit, altså typisk en ellipse, parabel eller hyperbel; for polynomier af højere grad fås mere komplicerede kurver. Tilsvarende bestemmes en algebraisk flade i rummet af ligningen \(g(x,y,z) = 0\), hvor \(g\) er et polynomium; et system af to sådanne ligninger bestemmer typisk en algebraisk rumkurve.
Det generelle system indeholder \(k\) ligninger af formen \(f_i(x_1,...,x_n)=0\) svarende til polynomierne \(f_1,...,f_k\) i \(n\) variable. Løsningsmængden, der altså består af de fælles nulpunkter \((x_1,...,x_n)\) for polynomierne \(f_i\), kaldes en affin algebraisk mangfoldighed. Algebraiske mangfoldigheder indgår i en række områder inden for matematikken og fysikken, fx i gaugeteori, superstrengteori, kryptologi og robotteknik.



Kommentarer
Kommentarer til artiklen bliver synlige for alle. Undlad at skrive følsomme oplysninger, for eksempel sundhedsoplysninger. Fagansvarlig eller redaktør svarer, når de kan.
Du skal være logget ind for at kommentere.