Mekanik, gren af fysikken, som behandler legemers bevægelse eller hvile. Kinematik beskriver bevægelse uden at inddrage de kræfter, som forårsager den, til forskel fra dynamik, som knytter bevægelsen af et materielt legeme til de kræfter og kraftmomenter, der påvirker det; statik beskriver hviletilstanden.
Faktaboks
- Etymologi
- Ordet mekanik kommer af græsk mechanike (techne), af mechanikos, af mechane 'redskab, værktøj' og -ik.
Mekanik beskriver fænomener i naturen og grunder sig som anden naturbeskrivelse på iagttagelser og eksperimenter. Nogle få fænomener kan beskrives i ord, men mekanik er præget af, at beskrivelsen i alt væsentligt må være matematisk; dette forhold blev tidligt fremhævet af Galilei, der kan betragtes som den matematiske mekaniks fader.
Mekanik anses for at være den mest fundamentale af fysikkens discipliner. Grundlæggende begreber som impuls, impulsmoment og energi stammer fra mekanikken, men har fundet bred anvendelse inden for andre områder af fysikken. Desuden har løsningen af mekaniske problemer ført til udvikling af mange væsentlige matematiske metoder.
Det følgende behandler især klassisk mekanik, som bygger på Newtons love, og som derfor også kaldes newtonsk mekanik. Den særlige mekanik, som gælder ved hastigheder nær lyshastigheden, behandles i relativitetsteorien, og mekanik for atomare systemer, som præges af kvantefænomener, i kvantemekanik.


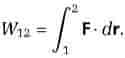



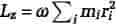
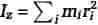






Kommentarer
Kommentarer til artiklen bliver synlige for alle. Undlad at skrive følsomme oplysninger, for eksempel sundhedsoplysninger. Fagansvarlig eller redaktør svarer, når de kan.
Du skal være logget ind for at kommentere.